行星运动的两个理想化模型

• 行星绕太阳的运动看作圆周运动，万有引力提供向心力
• 研究天体间的引力时，把天体看作质点

万有引力定律

推导：
1，太阳对行星的引力，引力提供向心力，所以
$$\begin{array}{cc}F=m\frac{v^2}{r}，且v=\frac{2\pi r}{T}& \\ 据开普勒第三定律，\frac{r^3}{T^2}=k\end{array}⟹F=4{\pi }^{2}k\frac{m}{r^2}⟹F\propto \frac{m}{r^2}$$
2，行星对太阳的引力
匀速圆周运动，根据牛顿第三定律
$$F^{\prime }=F\propto \frac{M}{r^2}$$
3，
$$F^{\prime }=F\propto \frac{Mm}{r^2}⟹F=G\frac{Mm}{r^2}$$
Tips:
$$F=4{\pi }^{2}k\frac{M}{r^2}⟹F=G\frac{Mm}{r^2}$$
G包含了k，
定义表达式：
$$F=G\frac{Mm}{r^2}$$
m,M为两物体质量，r为质点到质点（球心到球心距离），
G（Gravitationalconstant）为引力常量
由卡文迪许（Henry Cavendish，英）利用扭杆实验测出
$$G=6.67\times {10}^{-11}N\cdot m^2\cdot k{g}^{-2}$$

万有引力定律的应用

1，关于一个物体所受万有引力，在地球上的两个分力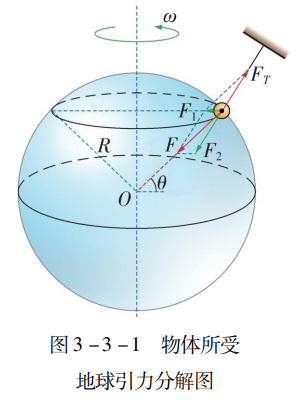

$$F=G\frac{Mm}{R^2}\{\begin{array}{cc}分力F_1=m{\omega }^{2}Rcos\theta ，物体随地球自转所需要的向心力& \\ 分力F_2：F_2与F_T平衡，为我们平时熟知的重力& \end{array}$$
因此，重力是万有引力在地球表面上的一个分力
对于重力与地球纬度的关系，有：
$$\begin{array}{cc}{F}_1=m{\omega }^{2}R\cos \theta ，R为地球半径，\theta 为地球纬度，\frac{1}{cos\theta }\propto \theta & \\ 同轴传动，\omega 恒定，F_1\propto cos\theta & \end{array}$$
由矢量三角形定则，万有引力恒定不变，F1变小，则F2（重力）变大
因此，g随纬度增加而增大，gmax在两极地区
而g随高度增大而减小（r=R+h）
2，计算天体质量
2.1“自立更生法”——G，R法
一定是天体表面上的物体质量为m，认为其万有引力约等于重力
$$G\frac{Mm}{R^2}=mg\Rightarrow M=\frac{g{R}^2}{G}$$
GM=gR2又被成为黄金代换式，R为地球半径
2.2“借助外援法”——环绕法
卫星环绕天体运行，万有引力提供向心力
$$\begin{array}{cc}G\frac{Mm}{r^2}=m\frac{4{\pi }^2}{T^2}r\Rightarrow M=\frac{4{\pi }^2{r}^3}{G{T}^2}& \\ V=\frac{4}{3}\pi R^3& \end{array}⟹\rho =\frac{M}{V}=\frac{3\pi r^3}{G{T}^2{R}^3}$$
r为轨道半径，R为天体半径，近地运动认为r=R（忽略h），需要看具体情况

地球第一，第二，第三宇宙速度

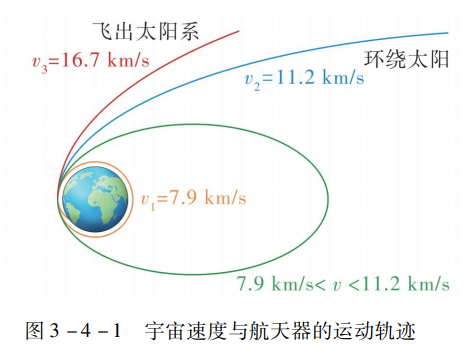
设地球质量为M，航天器质量为m，速度为v，到地心距离为r，使航天器发射并环绕地球做匀速圆周运动而不掉落，万有引力提供向心力
$$G\frac{Mm}{r^2}=m\frac{v^2}{r}\Rightarrow v=\sqrt{\frac{GM}{r}}$$
近地运动，r=R（地球半径），带入数据计算得v≈7.9km/s
因此，航天器在地球附近要地球做匀速圆周运动，所具有的速度必须为7.9千米每秒，称为宇宙第一速度或环绕速度
是航天器的最小发射速度，卫星环绕的最大速度
而v大于7.9km/s而小于11.2km/s，地球进入椭圆轨道
v>11.2km/s，摆脱地球引力被太阳捕获
v=11.2km/s，地球第二宇宙速度（逃逸速度），被太阳捕获
v=16.7km/s，地球第三宇宙速度，逃离太阳，飞出太阳系

同步卫星，近地卫星，赤道上的物体

| | 轨道半径 | 周期T | 向心力F | 备注 |
| ------------ | ------------ | ------------ | ------------ | ------------ |
| 赤道上的物体 | 地球半径 | 等于地球自转周期24h | 万有引力与支持力的合力 | 在赤道上与地球保持相对静止 |
| 近地卫星 | 地球半径 | T≈85min |万有引力 | 离地高度近似认为0，与地球有相对运动 |
| 赤道卫星 | h≈36000km | 等于地球自转周期24h | 万有引力| 轨道面与赤道面重合，与地球保持相对静止 |
向心加速度的比较，
a=GM/r2，同步卫星加速度小于近地卫星加速度
a=ω2r，同步卫星加速度大于赤道上的物体的加速度

关于同步卫星的一些参量（五同）

• 与地球自转方向一致，在赤道上空
• 与地球自转周期同T=24h
• 与地球角速度相同
• 定高度$$h={}^3\sqrt{\frac{GM{T}^2}{4{\pi }^2}}-R\approx 36000km$$

• 定线速度$$v=\sqrt{\frac{GM}{R+h}}=3.1km/s$$

  人造卫星速度比较

  都在宇宙中，万有引力提供向心力（前提）
  $$\{\begin{array}{cc}a=\frac{GM}{r^2}& \\ \omega =\sqrt{\frac{GM}{r^3}}& \\ v=\sqrt{\frac{GM}{r}}& \\ T=2\pi \sqrt{\frac{r^3}{GM}}& \end{array}$$
  a,ω,v随r增大而减小，T随r增大而增大，
  因此，高轨低速大周期

  卫星变轨

  变轨原理
  $$\begin{array}{cc}G\frac{Mm}{r^2}=m\frac{v^2}{r}匀速圆周运动& \\ G\frac{Mm}{r^2}>m\frac{v^2}{r}近心运动（变低轨）& \\ G\frac{Mm}{r^2}<m\frac{v^2}{r}离心运动（变高轨）& \end{array}$$
  低轨变高轨应加速变轨。高轨变低轨应减速变轨