曲线运动概念，性质

概念：物体的运动轨迹都是曲线的运动
（别于直线运动：直线运动的运动轨迹都是直线）


曲线运动的方向：
质点在某一位置的速度方向与曲线在这一点的切线方向一致
描述：沿着切线方向指向物体前进方向

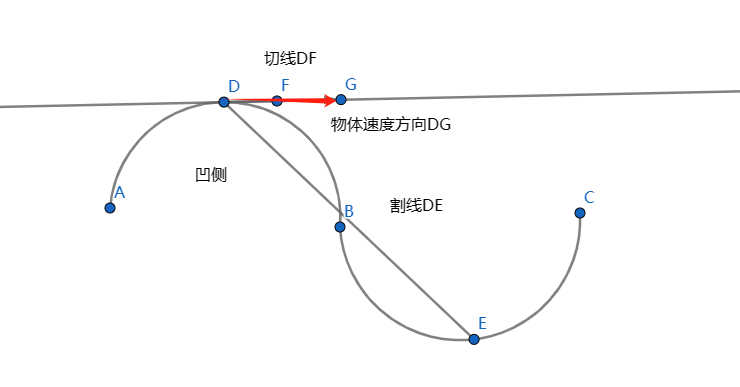
曲线运动过程中速度方向不断改变（大小不一定改变，方向一定改变），所以一定是变速运动⇔一定有加速度

曲线运动的条件

实验原理：力是改变物体运动状态的原因

当物体所受合外力（加速度）的方向与它的速度方向不在同一直线上时，即a,v不共线时物体做曲线运动，
（同理区别于直线运动：当物体所受合外力（加速度）的方向与它的速度方向在同一直线上时，即a,v共线时物体做直线运动）
曲线运动的受力特点

  • 合外力总是指向轨迹凹陷一边（重要依据）
  • 运动轨迹在合外力方向与速度方向的夹角必须小于180度之间

凹侧，加速度（合外力）方向示意图
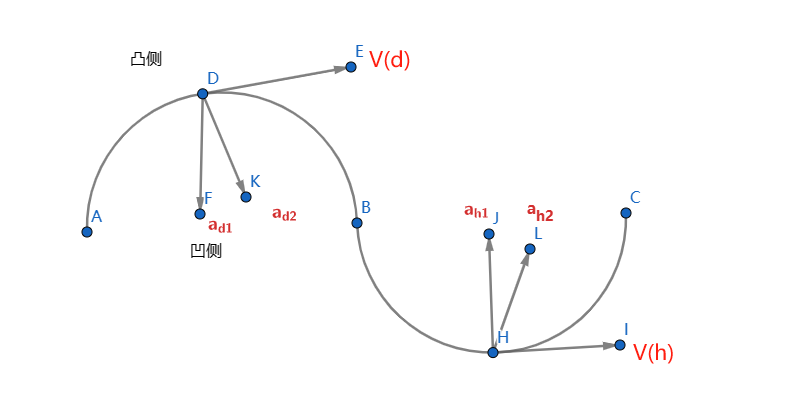
理论上有多个合外力方向，只要a,v夹角小于180°即可

其中如s-t,v-t图等二维图像，只能反映直线运动（因为这种图像只有两个方向，而曲线运动有无数个方向）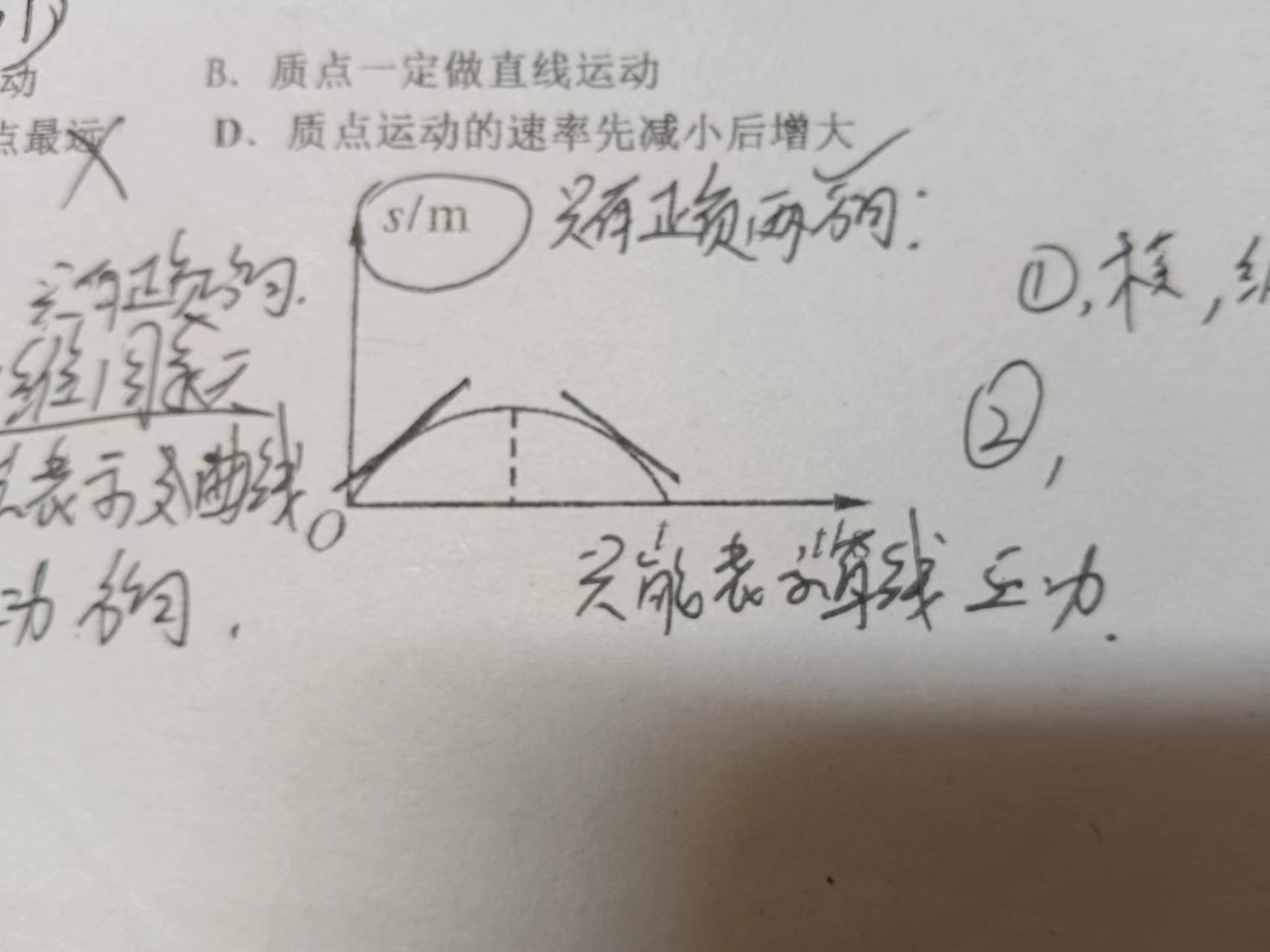

运动的合成与分解

定义：根据运动效果的等效性，把一个复杂的运动分解为两个或几个简单的运动进行分解（等效替代思想）
把一个物体实际的运动叫做合速度，把分解的两个运动叫做这个物体运动的分运动


数学原理：同一平面内，向量可以任意平移
实质：s,v,a的合成与分解

合运动与分运动的关系（分运动特性）

  • 等效性：各分运动的共同效果与和运动的效果相同
  • 等时性：各分运动与和运动同时发生，同时结束（所用时间相等）
  • 独立性：各分运动之间互不相干，彼此独立，互不影响
  • 同体性：各分运动与合运动是同一物体的运动

合运动性质判断

运动合成分解时，先合成/分解v,再合成/分解a

  • 互相角度的两个匀速直线运动的合运动，一定是匀速直线运动
  • 互成角度的一个匀速直线运动与匀变速运动的合运动,一定是匀变速运动
  • 互成角度的初速度为0的匀加速直线运动，一定是匀加速直线运动
  • 互成角度的两初速度不为零的匀变速直线运动的合运动，可能是匀变速直线运动或匀变速曲线运动

判断匀速/匀变：a是否恒定
判断加减速：
直线运动：a,v同向加速，反向减速
曲线运动：
a,v夹角<90° 加速
90°<a,v夹角减速<180°

最后修改：2024 年 03 月 02 日
© 允许规范转载
如果觉得我的文章对你有用，请随意赞赏