知识储备

• 向量a,b共线的一个充要条件是：存在唯一一个实数λ使$$\overrightarrow{b}=\lambda \overrightarrow{a}(\overrightarrow{a}\ne \overrightarrow{0})$$
• 任一向量基底表示具有唯一性：即

$$\{\begin{array}{cc}\overrightarrow{a}={\lambda }_1{\overrightarrow{e}}_1+{\lambda }_2{\overrightarrow{e}}_2& \\ \overrightarrow{a}={\mu }_1{\overrightarrow{e}}_1+{\mu }_2{\overrightarrow{e}}_2& \end{array}⟺\{\begin{array}{cc}{\lambda }_1={\mu }_1& \\ {\lambda }_2={\mu }_2& & \end{array}$$

结论与证明

存在实数m
使得
$$\begin{array}{rl}\overrightarrow{OA}=m\overrightarrow{OB}+(1-m)\overrightarrow{OC}& \\ \overrightarrow{OB}=m\overrightarrow{OA}+(1-m)\overrightarrow{OB}& \\ \overrightarrow{OC}=m\overrightarrow{OA}+(1-m)\overrightarrow{OB}& \end{array}$$
已知O,A,B三点不共线，且 O P → = m O A → + n O B → ( m , n ∈ R )，求证：A,P,B三点共线的充分必要条件是m+n=1
证明：
必要性：
$$\begin{array}{cc}若A,P,B三点共线，则\overrightarrow{BP}与\overrightarrow{BA}共线& \\ 存在实数\lambda 使\overrightarrow{BP}=\lambda \overrightarrow{BA},其中\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}& \\ \overrightarrow{OP}-\overrightarrow{OB}=\overrightarrow{BP}=\lambda (\overrightarrow{OA}-\overrightarrow{OB)}& \\ \overrightarrow{OP}-\overrightarrow{OB}=\lambda \overrightarrow{OA}-\lambda \overrightarrow{OB}& \\ \overrightarrow{OP}=\lambda \overrightarrow{OA}+(1-m)\overrightarrow{OB}& \\ \therefore m\overrightarrow{OA+n\overrightarrow{OB}=\lambda \overrightarrow{OA}+(1-\lambda )\overrightarrow{OB}}& \\ \therefore \{\begin{array}{cc}m=\lambda & \\ n=1-\lambda & \end{array}\therefore m+n=1\end{array}$$
充分性：
$$\begin{array}{cc}若m+n=1，则\overrightarrow{OP}=\overrightarrow{OA}+(1-m)\overrightarrow{OB},& \\ \overrightarrow{OP}=m\overrightarrow{OA}+\overrightarrow{OB}-m\overrightarrow{OB}& \\ \therefore \overrightarrow{OP}-\overrightarrow{OB}=m(\overrightarrow{OA}-\overrightarrow{OB})& \\ \therefore \overrightarrow{BP}=m\overrightarrow{BA}& \\ \therefore A,P,B三点共线& \end{array}$$

实例与应用

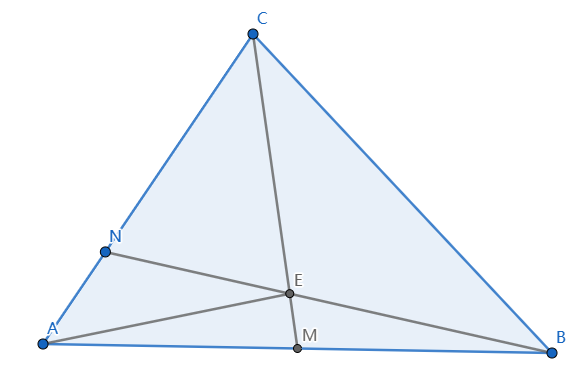
如图，三角形ABC中，M为AB中点，N为AC上的三等分点，BN与CM相交于E，设AB→=a→,AC→=b→，试用基底{a→,b→}表示向量AE→
$$\begin{array}{cc}\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AC}=\frac{1}{3}\overrightarrow{b}& \\ \overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}=\frac{1}{3}\overrightarrow{a}& \\ A,E,B三点共线，可知，存在M使& \\ \overrightarrow{AE}=m\overrightarrow{AN}+(1-m)\overrightarrow{AB}& \\ C,E,M三点共线，可知，存在M使& \\ \overrightarrow{AE}=m\overrightarrow{AM}+(1-m)\overrightarrow{AC}& \\ \therefore m\overrightarrow{AN}+(1-m)\overrightarrow{AB}=m\overrightarrow{AM}+(1-m)\overrightarrow{AC}& \\ \therefore m\frac{1}{3}\overrightarrow{b}+(1-m)\overrightarrow{a}=n\frac{1}{2}\overrightarrow{a}+(1-n)\overrightarrow{b}& \\ \{\begin{array}{cc}\frac{1}{3}m=1-n& \\ 1-m=\frac{1}{2}n& \end{array}& \\ \{\begin{array}{cc}m=\frac{3}{5}& \\ n=\frac{4}{5}& \end{array}& \\ \therefore \overrightarrow{AE}=\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}& \end{array}$$

“爪子模型”

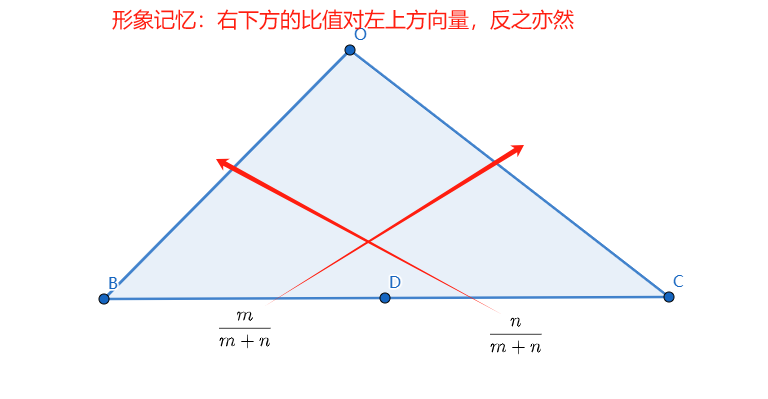
如图，D,B,C共线，D为BC的x等分点，即BD:DC=m:n
则有
$$\overrightarrow{OD}=\frac{n}{m+n}\overrightarrow{OB}+\frac{m}{m+n}\overrightarrow{OC}$$
应用：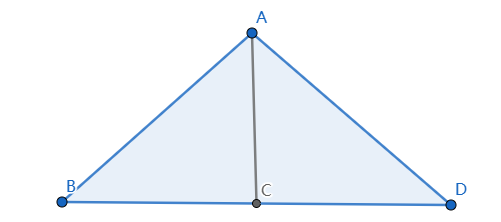

如图，C为BD中点，用AB→，AD→表示AC→
直接可得：
$$\overrightarrow{AC}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$$
常规方法验证：
$$\begin{array}{cc}\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}& \\ \overrightarrow{AC}=\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BD}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}& \end{array}$$

极化恒等式的证明

$$4\overrightarrow{a}·\overrightarrow{b}=(\overrightarrow{a}+\overrightarrow{b}{)}^2-(\overrightarrow{a}-\overrightarrow{b}{)}^2$$
证明：
如图，

2024 - 3-31 在月考中用到了！

题目：
我的解答：